À propos de l’article du Monde : Comment est calculée la mortalité liée à la pollution ? Ouvert aux commentaires.
De la mortalité causée par les PM2.5
Je tente d’expliquer à ma façon les chiffres sur la mortalité « évitable » par réduction des particules dites PM2.5, polluant connu et identifié.
Le corps médical s’accorde en assez grand détail sur la mortalité causée par les PM2.5, comptées en µg/m3. La figure ci-dessous est la Fig.1 extraite de l’article de 2015 « Addressing Global Mortality from Ambient PM2.5 » de Joshua S. Apte et al. (DOI: 10.1021/acs.est.5b01236, Environ. Sci. Technol. 2015, 49, 8057–8066) donne la mortalité assez précise par cause pour une « population type ». Je l’ai taggué pour avoir des éléments en français et pour faire voir quelques éléments saillants : non linéarité de la réponse dans la zone intéressante des villes polluées notamment.
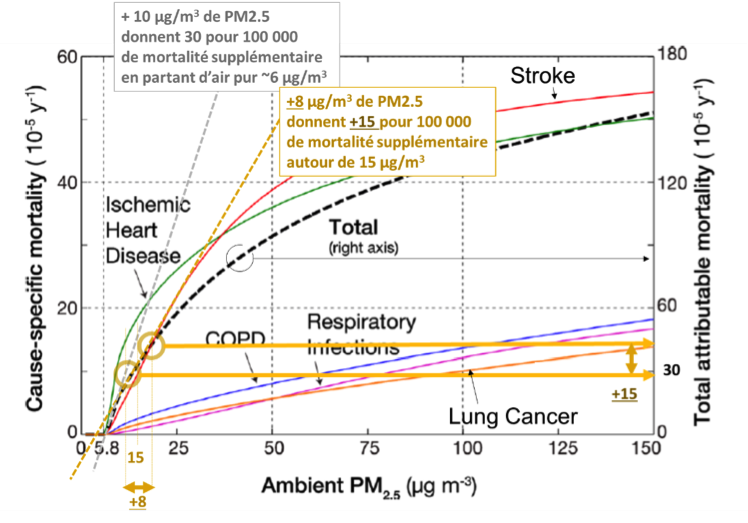
Mais passer de la mortalité à la « mortalité évitée » n’est pas évident pour les gens (comme moi) peu familiers avec l’épidémiologie. Par exemple, vers 30 µg/m3, on a une mortalité causée de 70/100 000. Pour une population de 60 000 000 qui subirait cette pollution, il faut multiplier ce chiffre de 70 par 600, ce qui donne 42 000. Le petit laïus qui suit aide à comprendre l’étude de Santé Publique France publiée le 21/06/2016, « Environnement et santé / Impacts de l’exposition chronique aux particules fines sur la mortalité en France continentale et analyse des gains en santé de plusieurs scénarios de réduction de la pollution atmosphérique ».
En effet, cette étude n’est hélas pas très pédagogique, ne serait-ce que les formules sont pour une partie quasi illisibles dans le pdf, et l’essentiel est dédié à soupeser le fait qu’il y a diversité de modèle et de maillage pour la pollution (urbaine, rurale, etc.) et pour les tranches d’âge des gens exposés dans ces différents cas (démographie précise), le tout en recoupant des données par commune, en s’assurant de la signification statistique (est-on sûr que 10 morts relevés sur 100 communes de 300 habitants sont sur le même pied qu’une commune de 30.000 habitants de même niveau de pollution, etc.).
Le point de base est que nous mourrons tous, donc que notre probabilité à 30 ans de mourir à un âge donné X est une courbe en cloche centrée quelque part vers 75-80 ans (l’espérance de vie). Psychologiquement, c’est plus facile de raisonner sur les tranches de cette zone (disons 78 ans) que sur celle de 35-40 ans par exemple, où l’on est rétif à imaginer la mortalité « naturelle ». Une fois que vous avez atteint 78 ans, vous avez donc une chance respectable de mourir dans l’année, en gros 14%, et donc 86% de survivre. Dans 7 ans (à 85 ans), comme 0.867 = 0.35, vous aurez perdu 65% de vos ami.e.s du même âge et gardé 35%.
J’ai utilisé là un modèle « exponentiellement décroissant », dont le taux de mortalité à un âge donné est constant. Il permet de raconter les choses facilement. La version la plus simple suppose qu’on ne meurt jamais jusqu’à 70 ans et qu’on a, abruptement, une chance sur 7 par an de mourir dans l’année, les 14% ci-dessus. Un tel modèle prédit les courbes vertes ci-dessous, qui ne sont pas trop irréalistes par rapport à la pyramide des âges (mieux pour les hommes, soit) :
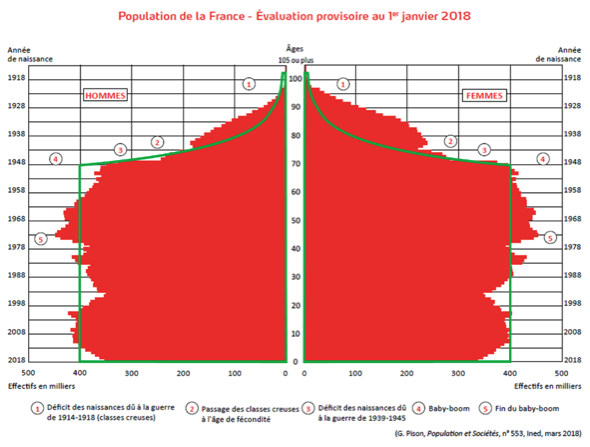
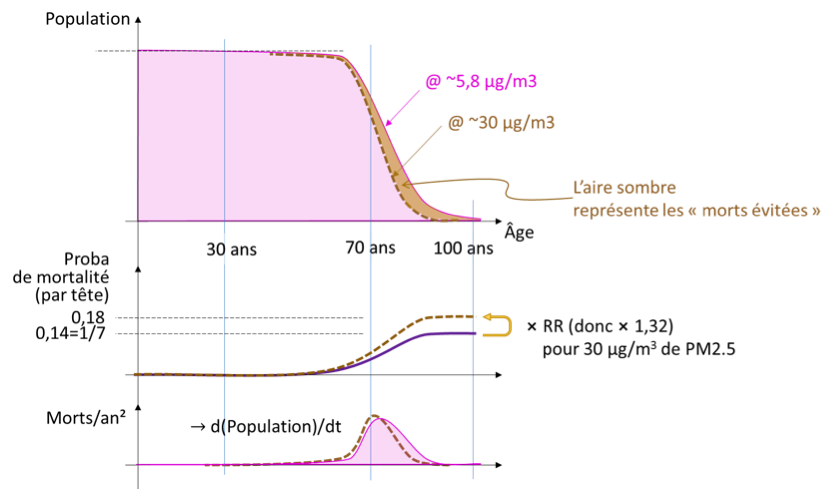
Muni de cette démographie simplifiée (population constante, taux de mortalité constant par an après 70 ans), on peut regarder les courbes violettes du graphe général de gens qu’on va appeler « vivant en air assez pur » ci-dessous, que je vais commenter (avant de passer aux cas de gens « affectés par les PM2,5 à une certaine dose » qui sera en marron pointillé) :
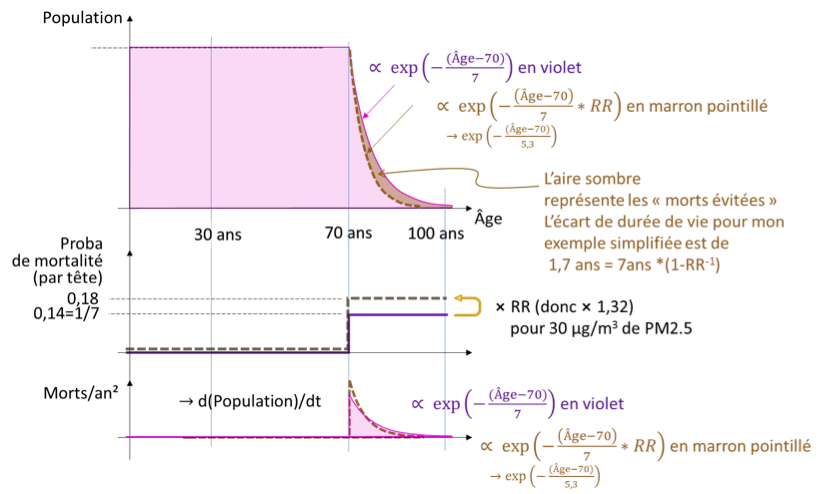
En haut, en violet donc, on retrouve la population par tranche d’âge, comme dans une pyramide, mais couchée à l’horizontale, avec la loi exponentielle de chute après 70 ans (la courbe violette est donc bien celle qui était verte sur les pyramides, on ne la voyait pas si je l’y laissais violette 🙁 , avec maintenant l’âge « en abscisse » : à l’horizontale).
Dans le graphe du milieu (même axe horizontal : âges), le « taux de mortalité » est la courbe violette, celle qui fait une forme de « marche d’escalier», et passe d’un coup de 0 à 0,14 (1/7ième) à 70 ans.
Dans le graphe du bas : le nombre de morts par an est une quantité importante, puisque c’est à cette quantité qu’on se doit de comparer en premier les mortalités dues à la pollution. Dans le modèle simple et de population stable, cette quantité de morts est la pente de la courbe du haut (les morts à 73 ans sont la différence entre vivants à 74 ans et vivants à 73 ans) et donc au signe près, c’est la dérivée mathématique de la population -d(Population)/dt. Le nombre de morts par an suit ici la même loi exponentielle que la population, c’est l’avantage de modéliser avec ce genre de loi. Ici, il s’agit d’une loi en exp{-(Age-70)/7} [pour Age >70] dans les deux cas. Donc spécifiquement pour mon modèle, les courbes ont la même allure décroissante très classique.
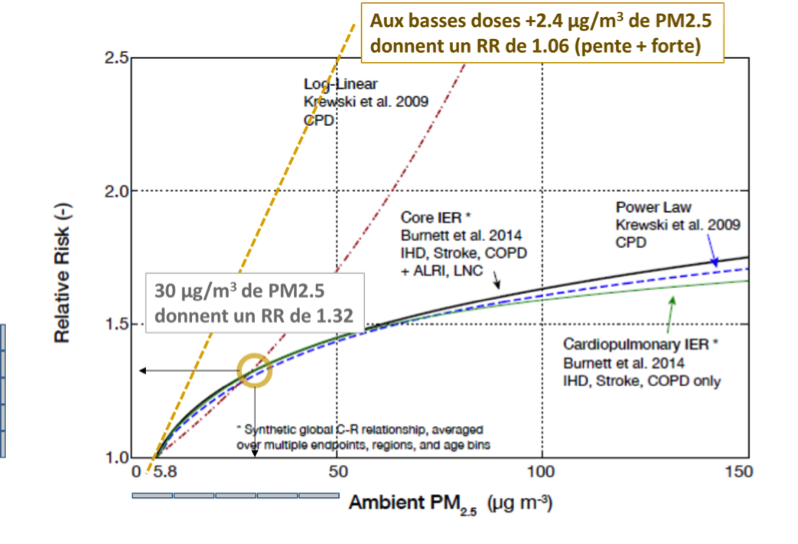
Là-dessus, les épidémiologues transforment les mortalités observées (Fig.1) en RR : « Risk Ratio », ou en français « Risque Relatif ». Une population donnée voit son taux de mortalité multiplié par ce facteur RR lié aux PM2.5. Dans le supplément de l’article suscité de Joshua S. Apte et al. On trouve en Fig. SI1 cette courbe qui est « la bonne » à mon avis, et qui est indépendante de l’âge : les PM2.5 « tuent autant » quel que soit l’âge (>30 ans je crois toutefois …).
La forme de la courbe s’explique bien par la mortalité observée, mix de certaines causes sensibles à faible dose (maladies cardiaques) et d’autres moins (cancer des poumons). Le modèle violet dit « Log-linear » (point-trait-point) a été exclu il y a quelques années, donnant des RR irréalistes (> 2) aux forts PM2.5. Pour ces fortes concentrations, on s’est basé sur des cas particuliers (maisons enfumées, industries particulières) pour vérifier que, bon an mal an, les gens « résistent » aux fortes doses, et que le « poison » est surtout ‘efficace’ (en relatif) aux faibles doses.
J’ai tracé par-dessus la pente à l’origine (pointillé marron et encart au-dessus), qui est en gros deux fois plus forte que la pente locale vers 30 µg/m3 : si vous avez une machine miraculeuse qui enlève 3 µg/m3 de PM2.5, utilisez là pour dépolluer une ville d’assez bon air (10 µg/m3) plutôt que Milan aux mauvaises heures, vous sauveriez plus de vies !! Bien sûr, côté émission, c’est l’inverse : il est plus facile, si on croit encore en un État régulateur du moins, de repérer et d’inciter les « gros pollueurs » (usines, diesel…) que la myriade d’activités polluant à bas bruit (barbecue, usure de freins, chantiers, chauffage gaz « assez propre »…).
Nous allons raisonner sur le point à 30 µg/m3 : il est associé à un RR de 1,32 : la mortalité des gens est 1,32 fois plus importante que sans les PM. Encore faut-il qu’ils meurent ! Dans mon modèle de gens inoxydables jusqu’à 70 ans, la conséquence de ce RR est nulle jusqu’à 70 ans ! C’est là le point qui fait que « personne ne connait quelqu’un mort de la pollution ». C’est une cause qui « se rajoute multiplicativement » ; si, comme on dit dans certains coins de l’Ouest, « Il y a le vieux qui rentre » en vous, ou si comme dirait Brassens, vous êtes déjà un peu « guetté par la Camarde », vous lui entrouvrez la porte un peu plus avec les PM. Mais de 30 à 70 ans (dans mon modèle) on ne voit rien de rien.
La suite est assez simple. Puisque vous avez 1,32 fois plus de chance de mourir, le 14% devient 14 x 1,32=18% à peu près. On doit donc se baser sur la courbe en échelon en pointillé marron. Dans ce cas, le facteur de décroissance de l’exponentielle est de 5,3 ans au lieu de 7 ans. (1/0,18 au lieu de 1/0,14 aux arrondis près). La chute en pointillé marron est donc plus rapide dans la population. Et la mortalité (graphe du bas) est une courbe pointue mais qui a son pic plus haut et plus étroit.
Formellement, la population totale n’est pas constante dans mon modèle : la tranche entre la courbe pointillée (30 µg/m3) et la courbe « bon air » violette est une différence de population. Ça joue sur 2%, et ce n’est pas grave pour la suite en tant que tel. En revanche, en laissant la courbe telle quelle, on a sous les yeux le fameux « NOMBRE DE MORTS ÉVITÉES » : c’est tout bonnement la surface entre les deux courbes. Donc c’est 2% de la population, justement. Ou encore c’est la différence d’espérance de vie, qui est raccourcie de 7 ans à 5,3 ans, soit 1,7 ans (7 ×(1-RR-1)).
(Avec ce modèle exponentiel décroissant, la différence de taux devient une différence de population, intégrales et dérivées se réfèrent toutes aux mêmes exponentielles…).
Voilà donc les « morts évitables ». Si nous sommes actuellement dans la situation « mauvaise » (marron pointillé) et qu’on supprime brutalement la cause, on va passer à la situation bonne (violet continu) et gagner sur l’espérance de vie. Donc ces « morts évitées » sont « seulement » retardées de 1,6 ans, cela va accroître la population un petit peu (~2%). Les autres causes de variations démographiques (naissances, solde migratoire) sont bien plus fortes que ce « bruit ».
La réduction n’a en réalité pas d’effet immédiat, c’est évident pour les cancers, et un peu moins pour les maladies cardiaques, mais quand même. Donc même si un gros vent d’ouest salvateur soufflait sur la France 24/24 365 jours par an, il faudrait 15 ou 20 ans pour « ressusciter » ces morts, on n’en « gratterait » qu’un petit dixième la première année, etc.
Sur le chiffre absolu, il faut bien sûr pondérer, comme le fait l’étude « Santé Publique France », et on ne part pas de RR aussi élevés que 1,32 sauf dans un petit nombre de cas. Le résultat est que les gens en zone polluées gagneraient 0,8 ans, et en moyenne sur la France 0,4 an. 0,4 an rapporté à 80 ans, c’est 0,5%, donc rapporté à la population française de 67 000 000, c’est 34.000, on retrouve bien les chiffres annoncés.
Le détail dépend bien sûr des courbes réelles et de toute la démographie et de toute la répartition des PM, dans l’espace et le temps (si je passe à la gare du Nord 1 h par jour, combien ça compte ?).
A titre de pédagogie finale (si vous avez tenu jusqu’ici), voici les allures un peu plus réalistes que le modèle exponentiel, faites « à la main » : on y retrouve les mêmes tendances, sauf que les allures des transitions sont émoussées. A noter l’avance du pic de mortalité annuelle (en bas), puisque le modèle ne « coupe » plus abruptement à 70 ans. Et à noter que ce pic est le plus souvent un peu avant l’espérance de vie, puisque quand il ne reste plus que la moitié des gens, ils font moins de morts que au plus raide de la descente.
En résumé, il ne me semble pas qu’il y ait faute de raisonnement, mais faute de compréhension de qui gagne ces « morts évitées » : en résumé rapide : les vieux, et en résumé plus précis, ceux qui sont à l’âge de l’espérance de vie, soit vers 80 ans. En gros et un peu cruellement, les octogénaires seront les principaux bénéficiaires, pas les régimes de retraite ni celui de la sécu (quasiment pas d’année travaillée en plus). Et ceux des environnements peu pollués seront en nombre et à baisse absolue de PM, les plus grands bénéficiaires (c’est pour voir si vous vous rappelez du début : la courbe de réponse dite « C-R » est non linéaire !)
Cela n’enlèvera pas les moult bizarreries qu’on pourra trouver dans le grand tout statistique. Par exemple, dans l’étude de Santé Publique France, Annexe 2, tableau 1, il y a la comparaison entre Languedoc Roussillon (LcRn) et Ile de France (IdF), lors de l’étude pilote.
Décès annuels moyens (30 ans et plus) : 68 978 (IdF) et 24 977 (LcRn) .
C’est plus en LcRn en proportion de la population 6,9 et 1,7 millions donc : 1% et 1,5% en gros. C’est sans doute que les franciliens vivent un peu plus vieux d’une part, et partent mourir ailleurs sans doute (au sud notamment).
Or c’est LcRn qui a, assez nettement, le plus petit pourcentage de morts par maladie cardiovasculaire et respiratoire, alors qu’IdF est incontestablement plus polluée, surtout ramené à là où les gens vivent bien sûr (Paris et petite couronne). Les chiffres bruts sont en effet :
-> Décès cardiovasculaire annuels moyens (30 ans et plus) 16.654 (IdF) et 7.038 (LcRn)
-> Décès respiratoires annuels moyens (30 ans et plus) 4.173 (IdF) et 1.578 (LcRn)
Soit en pourcentage des 30 ans et plus (6,9 millions(IdF) 1,7 millions(LcRn))
=> Décès cardiovasculaire annuels moyens (30 ans et plus) 24,1% (IdF) et 28,7% (LcRn)
=> Décès respiratoires annuels moyens (30 ans et plus) 6,04% (IdF) et 6,32% (LcRn).
De quoi donner envie à un lobbyiste pollueur d’argumenter que « vous voyez, ça n’y est pour rien ». La réponse (négative !) à cette question est dans la (les) méta-études que Santé Publique France a dûment compilées en 2016, évidemment.
Au final : Le sujet n’est donc pas très simple et manque (manquait ?) de représentation graphique.
Le sujet délicat plus général de « donner les bonnes représentations graphiques » aux gens (avec ou sans gilets, de toute couleur) pour qu’ils puissent participer aux grandes décisions sur le climat et le cadre de vie mérite aussi de gros efforts, avis aux gens intéressés : ça m’intéresse !
Laisser un commentaire