J’ai déjà eu l’occasion de parler des modèles utilisés en finance. J’ai évoqué par exemple dans Les modèles financiers “scientifiques”, et les autres, la distinction faite par la profession entre les modèles dits « scientifiques » et ceux dits de « norme sectorielle » dont les imperfections sont connues mais qui sont utilisés à défaut d’une alternative plus satisfaisante. J’ai souligné à propos de ces derniers, le risque « systémique » qui leur est attaché du fait que le mécanisme qu’ils supposent est incorrect et que leur utilisation simultanée par un grand nombre d’acteurs dispose du coup de la capacité à déclencher une catastrophe. On a ainsi pu observer récemment qu’un certain nombre de « hedge funds », ces fonds d’investissement spéculatifs, avaient connu des pertes équivalentes du fait que leurs modèles partageaient la même hypothèse injustifiée d’une absence de corrélation entre différents produits financiers que la détérioration de la finance avait précisément fait réagir à l’unisson. J’ai aussi rappelé que bien des modèles financiers accordent une confiance abusive à leur prétention de prévoir l’avenir.
Dans un autre billet, intitulé celui-ci Le talon d’Achille des agences de notation, j’attirais l’attention sur le fait que les méthodes utilisées par les agences de notation (telles Standard & Poor’s, Moody’s et Fitch) qui évaluent le crédit des compagnies et des instruments de dette qu’elles émettent, supposent que de nombreux processus se produisent de manière purement aléatoire alors qu’ils sont en réalité pseudo–cycliques et que les phases où l’application de ces méthodes est valide alternent avec d’autres où elles ne le sont pas. J’écrivais à propos de ces agences qu’
… elles accumulent les données pour une population spécifique sur des périodes les plus longues possibles et produisent à partir de là une note individualisée qui équivaut à une probabilité de défaillance, de prépaiement, etc. Le rendement serait relativement bon s’il s’agissait de prévoir des événements rares dont l’occurrence n’est pas influencée par un climat général, par exemple le risque que vous mettiez accidentellement le feu à votre logement, mais quand il s’agit d’évaluer, comme dans le cas du crédit immobilier, votre capacité à rembourser sur trente ans un prêt de 600.000 euros consenti pour l’achat d’une maison, ça ne marche pas très bien, parce que cette capacité ne dépend pas uniquement de vous mais aussi, et de manière déterminante, de ce que sera la conjoncture économique durant ces trente années à venir. Et c’est là que se situe le talon d’Achille des agences de notation.
Une illustration empruntée au texte des auteurs qui, à ma connaissance, furent les premiers à signaler cette faiblesse, Raynes et Rutledge (1), montre très clairement la propension de cette faiblesse à se transformer en erreur flagrante lorsque le processus n’est pas purement aléatoire ou est cyclique comme dans l’exemple représenté.
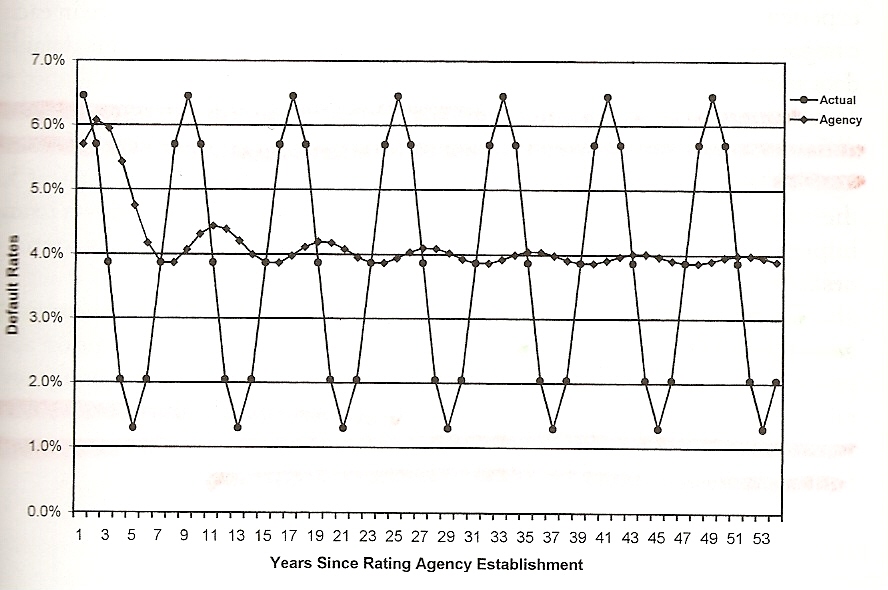
Comme je viens de le rappeler, les notateurs collectent les séries chronologiques les plus longues possibles et, lorsque les observations peuvent se poursuivre, ajoutent consciencieusement les nouvelles à la suite des plus anciennes pour constituer une série chronologique. Si l’on a affaire à un processus cyclique, voyons ce que le diagramme révèle : tant que l’on en est au début de l’enregistrement des données, une extrapolation à partir des premières observations permet de bien « coller » à la réalité mais plus la série s’allonge, moins la prévision est bonne. Pire, alors que la qualité de la prévision se détériore manifestement, sur un plan mathématique, son rendement semble s’améliorer par le simple allongement de la série et du fait que la probabilité est définie comme un passage à la limite des fréquences observées. Notons que des modèles de prévision des défaillances beaucoup moins sophistiqués sur le plan mathématique, comme celui de Robert C. Merton, qui se contentent d’évaluer la solvabilité d’une compagnie en comparant son passif et son actif, ne présentent pas ce défaut.
Dans un article paru avant–hier dans Les Échos et intitulé La finance est anormale, Jean-Marc Vittori rappelle que le fameux modèle de Black et Scholes utilisé pour la valorisation des options financières repose sur la supposition que le processus sous–jacent présente une distribution dite « normale » : celle qui correspond à la fameuse représentation de la « courbe en cloche ». La distribution « normale » caractérise les processus aléatoires les plus sympathiques car les plus prévisibles, ce que j’appellerais l’« aléatoire apprivoisé » où, par exemple, le « mode », le cas le plus commun et la « médiane », la valeur qui laisse la moitié (moins elle) des données à sa droite et la moitié (moins elle) à sa gauche, coïncident tous deux avec la « moyenne », et autres propriétés accommodantes qui nous facilitent la vie.
Ceci dit, le fait que le modèle de Black et Scholes suppose une distribution « normale » est un péché véniel par rapport à une anomalie beaucoup plus sérieuse et qui aurait dû faire qu’il ne soit jamais utilisé avant que celle–ci ne soit éliminée : ce qu’on appelle le « sourire » – du fait que l’anomalie apparaît sous cette forme sur un diagramme – qui reflète le fait que la volatilité du produit sous–jacent à l’option présente des valeurs différentes selon le niveau de prix auquel l’option est située par rapport au prix actuel de produit. La volatilité du produit sous–jacent, c’est–à–dire la disposition de son prix à varier, n’a bien sûr qu’une seule valeur, et le phénomène du « sourire » révèle une erreur pure et simple au sein du modèle de Black et Scholes. J’ai eu l’occasion de montrer autrefois (en 1995) que l’erreur est due au fait qu’il manque une variable au modèle : le profit du « vendeur » de l’option, et que cette dimension manquante se trouve du coup agrégée avec la variable « flottante » appelée « volatilité », avec laquelle elle n’a bien entendu rien à voir (2).
Tout ceci nous rappelle à point nommé que la finance moderne navigue périlleusement entre le Charybde des modèles que nous savons incorrects et auxquels nous recourons quand même après les avoir qualifiés de « norme sectorielle » et le Scylla des modèles que nous imaginons corrects et qui ne le sont pas !
(1) Raynes, Sylvain & Rutledge, Ann, The Analysis of Structured Securities. Precise Risk Measurement and Capital Allocation, Oxford : Oxford University Press, 2003
(2) J’ai ré–expliqué cela dans l’un de mes billets récents en anglais The smile in Black and Scholes (Le sourire dans Black et Scholes)
5 réponses à “Les modèles financiers entre Charybde et Scylla”
Bonjour,
Effectivement,
Utilisée une distribution normale sert seulement d’outil pour approximer au maximum le prix d’une option.
Il ne s’agit pas de certitude mais juste d’approximation.
Si quelqu’un apporte un meilleur outil approximatif, il serait utile de le présenter.
pierre
Mandelbrot a apporté une meilleure théorie avec les fractales. le problème c’est que ça conduit à une modélisation complexe; tellement plus complexe à mettre en oeuvre que tout le monde préfère Black and Scholes, simple…. mais non exact pour les évènements « rares » et extrêmes du marché.
[…] le prix d’une option. J’ai déjà évoqué cette formule et ses problèmes dans Les modèles financiers entre Charybde et Scylla. Je rappelle brièvement que la formule est très inexacte : il lui manque une variable qui […]
[…] pour calculer le prix d’une option. J’ai déjà évoqué cette formule et ses problèmes dans Les modèles financiers entre Charybde et Scylla. Je rappelle brièvement que la formule est très inexacte : il lui manque une variable qui […]
tout modèle ne représente une valeur qu’ en ce qu’ il permet de s’ expliquer un phénomène réel en le simplifiant il est clair que le modèle ne peut êre tenu pour responsable de la mauvaise utilisation qui en est faite black csholès donne une appréciation d’ une valeur probable à comparer déjà aux valeurs de marché pour prendre sa décision d’ achat ou de vente ce faisant on sait déjà que si les biais de la période ne sont pas importants on peut espérer avoir pris une bonne décision
il faut garder à l’ esprit que ceci n’ est que probabilité et que sa part d’ analyse personnelle de ce qui est trop complexe à modéliser ,reste déterminante afin d’ éviter les erreurs vous êtes dans un avion dans les nuages , vous disposez d’ un compas d’ un indicateur de virage , d’ un taux de descente ou montée , ceci ne vous dit pas si vous êtes sur le dos , c’ est sensation de douleur due à la ceinture qui vous le fait . plus grave l’ altimètre dépendant de votre analyse des données de pression à lui communiquer , l’ erreur peut même vous tuer malgré son excellent fonctionnement